Die lineare Regression modelliert eine Beziehung zwischen abhängigen y und unabhängigen x statistischen Datenvariablen. Mit anderen Worten, sie markieren einen Trend zwischen zwei Tabellenspalten in einer Tabelle. Wenn Sie z. B. eine Excel-Tabelle mit einer Spalte "Monat x" einrichten und eine Datenmenge für jeden der Monate in der benachbarten y-Spalte erfassen, hebt die lineare Regression den Trend zwischen den Variablen x und y durch Hinzufügen von Trendlinien zu Tabellengrafiken hervor . So können Sie Excel-Grafiken eine lineare Regression hinzufügen.
Hinzufügen einer linearen Regressions-Trendlinie zum Graphen
Öffnen Sie zuerst eine leere Excel-Tabelle, wählen Sie die Zelle D3 und geben Sie als Spaltenüberschrift "Monat" ein. Dies ist die x-Variable. Klicken Sie dann auf Zelle E3 und geben Sie Y-Wert als Spaltenüberschrift y ein. Dies ist im Grunde eine Tabelle mit einer aufgezeichneten Reihe von Datenwerten für die Monate Januar-Mai. Geben Sie also die Monate in den Zellen D4 bis D8 und die Datenwerte für sie in den Zellen E4 bis E8 ein, wie in der Momentaufnahme direkt unten gezeigt.
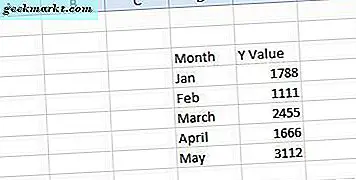
Jetzt können Sie ein Streudiagramm für diese Tabelle einrichten. Markieren Sie alle Zellen in der Tabelle mit dem Cursor. Klicken Sie auf die Registerkarte Einfügen, und wählen Sie Scatter > Scatter nur mit Markern aus, um das Diagramm der Tabelle wie folgt hinzuzufügen. Alternativ können Sie auch die Tastenkombination Alt + F1 drücken, um ein Balkendiagramm einzufügen. Dann sollten Sie mit der rechten Maustaste auf das Diagramm klicken und Diagrammtyp ändern > XY (Scatter) > Scatter nur mit Markern auswählen.
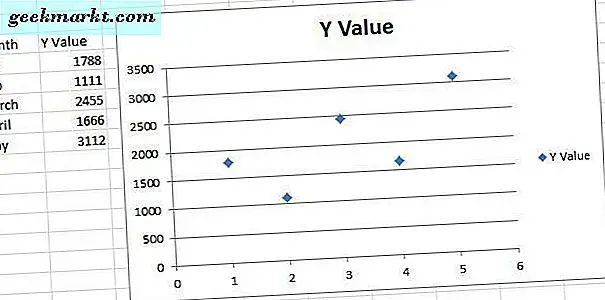
Wählen Sie als Nächstes einen der Datenpunkte im Streudiagramm und klicken Sie mit der rechten Maustaste, um das Kontextmenü zu öffnen, das die Option Trendlinie hinzufügen enthält. Wählen Sie Trendlinie hinzufügen, um das Fenster zu öffnen, das im Schnappschuss direkt darunter angezeigt wird. Dieses Fenster enthält fünf Registerkarten mit verschiedenen Formatierungsoptionen für Trendlinien der linearen Regression.
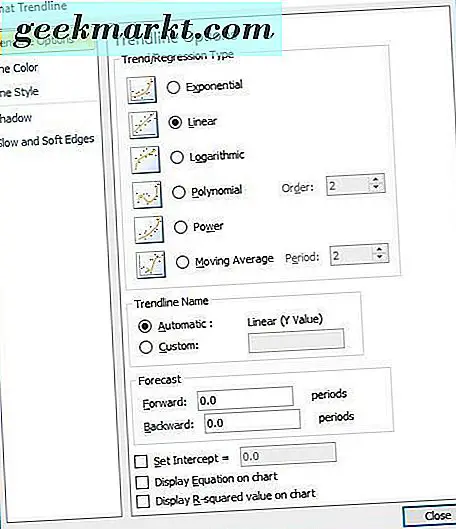
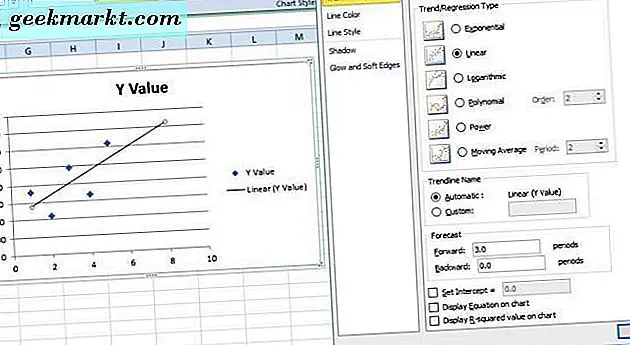
Klicken Sie zuerst auf Trendlinienoptionen und wählen Sie einen Regressionstyp aus. Sie können die Optionen Exponential, Linear, Logarithmisch, Moving Average, Power und Polynomial- Regressionstyp von dort auswählen. Wählen Sie " Linear" und klicken Sie auf " Schließen", um diese Trendlinie dem Diagramm direkt hinzuzufügen.
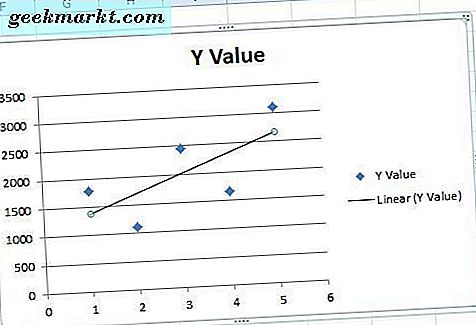
Die Liner-Regressions-Trendlinie in der obigen Grafik hebt hervor, dass es eine allgemeine Aufwärtsbeziehung zwischen den x- und y-Variablen gibt, trotz einiger Tropfen auf dem Chart. Beachten Sie, dass die Trendlinie der linearen Regression keine der Datenpunkte im Diagramm überlagert. Sie ist also nicht mit Ihrem durchschnittlichen Liniendiagramm identisch, das jeden Punkt verbindet.
Formatierung der linearen Regressionslinie
Um die Trendlinie zu formatieren, klicken Sie mit der rechten Maustaste darauf und wählen Sie Trendlinie formatieren. Dadurch wird das Fenster Format Trendline erneut geöffnet, und Sie können auf Linienfarbe klicken. Wählen Sie die durchgezogene Linie und klicken Sie auf das Feld Farbe, um eine Palette zu öffnen, aus der Sie eine alternative Farbe für die Trendlinie auswählen können.
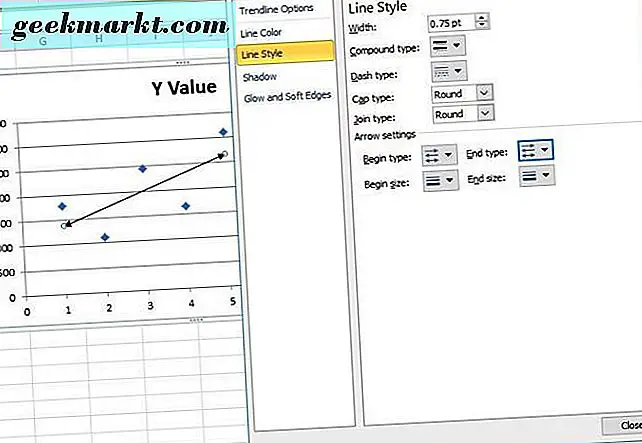
Um den Linienstil anzupassen, klicken Sie auf die Registerkarte Linienstil. Dann können Sie die Pfeilweite anpassen und die Pfeileinstellungen konfigurieren. Drücken Sie die Pfeiltasten, um der Linie Pfeile hinzuzufügen.
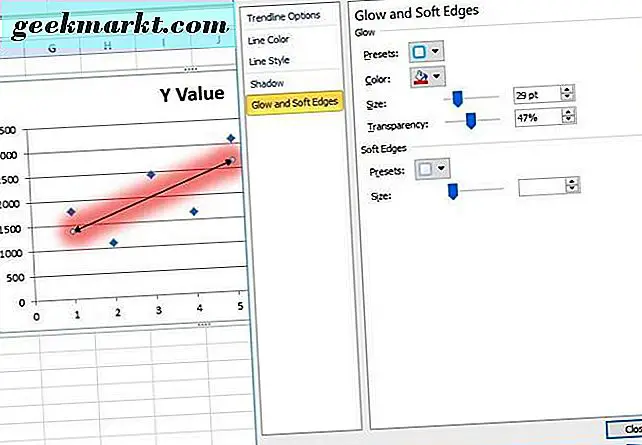
Fügen Sie der Trendlinie einen Glüheffekt hinzu, indem Sie auf Glühen und weiche Kanten klicken. Dadurch öffnet sich die Registerkarte, unter der Sie durch Klicken auf die Schaltfläche " Voreinstellungen" leuchten können. Wählen Sie dann eine Leuchtvariante, um einen Effekt auszuwählen. Klicken Sie auf Farbe, um alternative Farben für den Effekt auszuwählen, und ziehen Sie die Größen- und Transparenzbalken, um das Trendlinienglühen weiter zu konfigurieren.
Vorhersage von Werten mit linearer Regression
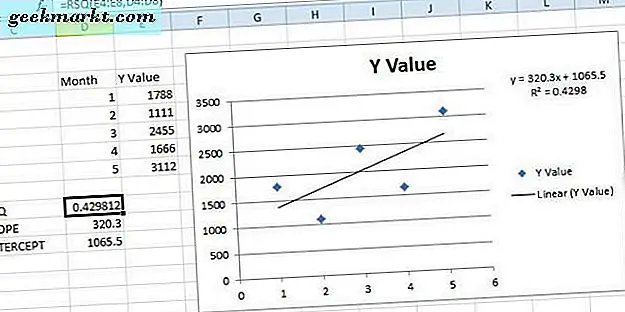
Sobald Sie die Trendlinie formatiert haben, können Sie auch zukünftige Werte damit prognostizieren. Angenommen, Sie müssen einen Datenwert drei Monate nach Mai für August prognostizieren, der in unserer Tabelle nicht enthalten ist. Dann können Sie auf Trendlinienoptionen klicken und "3" in das Textfeld "Weiterleiten" eingeben. Die Trendlinie der linearen Regression hebt hervor, dass der August-Wert wahrscheinlich knapp über 3.500 liegen wird, wie unten gezeigt.
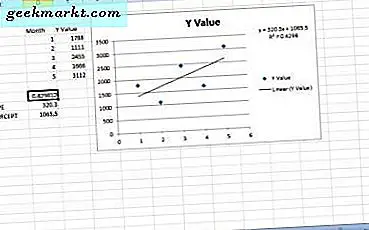
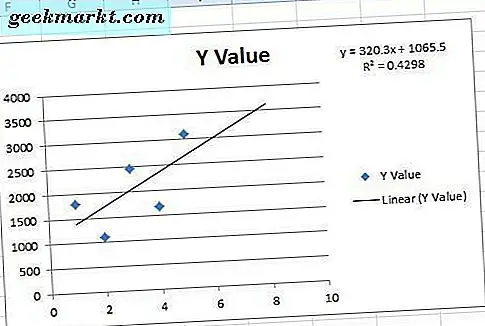
Jede lineare Regressions-Trendlinie hat ihre eigene Gleichung und einen quadratischen Wert, den Sie dem Diagramm hinzufügen können. Klicken Sie auf das Kontrollkästchen Gleichung für Diagramm anzeigen, um die Gleichung dem Diagramm hinzuzufügen. Diese Gleichung enthält eine Steigung und einen Schnittpunktwert.
Um den r-Quadratwert zum Diagramm hinzuzufügen, klicken Sie auf das Kontrollkästchen R-Quadrat-Wert im Diagramm anzeigen . Das addiert sich zu dem Diagramm direkt unterhalb der Gleichung, wie in dem folgenden Schnappschuss. Sie können das Formel- und Korrelationsfeld ziehen, um seine Position im Streudiagramm zu ändern.
Die linearen Regressionsfunktionen
Excel enthält auch lineare Regressionsfunktionen, die die Werte für Steigung, Achsenabschnitt und r-Quadrat für y- und x-Datenfelder enthalten. Wählen Sie eine Tabellenkalkulationszelle aus, der Sie eine dieser Funktionen hinzufügen möchten, und drücken Sie dann die Funktionstaste Einfügen . Die linearen Regressionsfunktionen sind statistisch. Wählen Sie daher im Dropdown-Menü Kategorie die Option Statistisch . Dann können Sie RSQ, SLOPE oder INTERCEPT auswählen, um ihre Funktionsfenster wie unten zu öffnen.
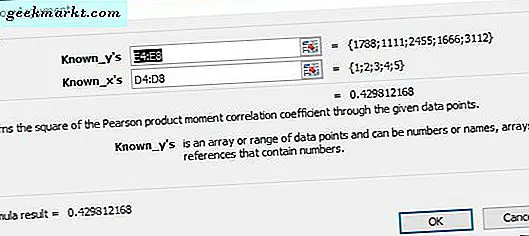
Die Fenster RSQ, SLOPE und INTERCEPT sind fast identisch. Sie enthalten die Felder Known_y und Known_x, die Sie auswählen können, um die y- und x-Variablenwerte zu Ihrer Tabelle hinzuzufügen. Beachten Sie, dass die Zellen nur Zahlen enthalten müssen. Ersetzen Sie daher Monate in der Tabelle durch entsprechende Zahlen wie 1 für Jan, 2 für Feb usw. Klicken Sie dann auf OK, um das Fenster zu schließen und die Funktion der Tabelle hinzuzufügen.
Jetzt können Sie Ihre Excel-Tabellen mit linearen Trendlinien verfeinern. Sie werden die allgemeinen Trends für die Datenpunkte von Graphen hervorheben, und mit den Regressionsgleichungen sind sie auch nützliche Prognosewerkzeuge.